Are The Events A And B Independent? Exploring Dependence In Probability
Derivation To Prove The Combination Of Compliment Events Are Also Independent
Keywords searched by users: Are the events A and B independent Show that if the events A and B are independent events then so are the events, Independent events, Dependent and independent events, Statistically independent events, How to prove 2 events are independent, The events A and B are not independent if, Given events A and B with probabilities P A 0.5 P B 0.4 and P A and B 0.2 are A and B independent, p(a and b)
Are Events A And B Dependent Or Independent?
Are events A and B dependent or independent? To determine the relationship between two events, we need to consider their independence or dependence. Events A and B are considered independent when the occurrence of one event has no impact on the probability of the other event happening. In contrast, if the occurrence of one event does influence the probability of the other event occurring, then events A and B are considered dependent. In simpler terms, the independence of events means that they occur independently of each other, while dependence implies that the occurrence of one event can affect the likelihood of the other event taking place. This distinction helps us analyze and understand the interplay between events in various situations.
Is A And B Are Two Independent Events?
Is it possible for events A and B to be considered independent of each other? To clarify, events A and B are deemed independent when the outcome or absence of one event does not influence the likelihood of the outcome or absence of the other event. In other words, the occurrence or non-occurrence of event A has no bearing on the probability of event B, and vice versa. This concept is fundamental in probability theory and helps us analyze situations where multiple events are at play, with each event having no impact on the other’s probability.
Top 28 Are the events A and B independent






Categories: Update 22 Are The Events A And B Independent
See more here: khoaluantotnghiep.net

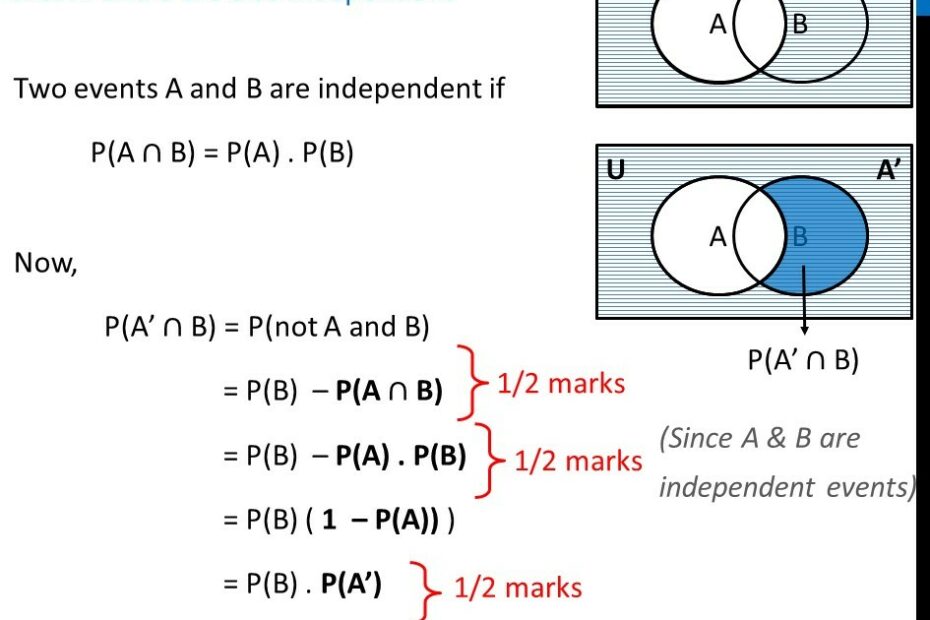
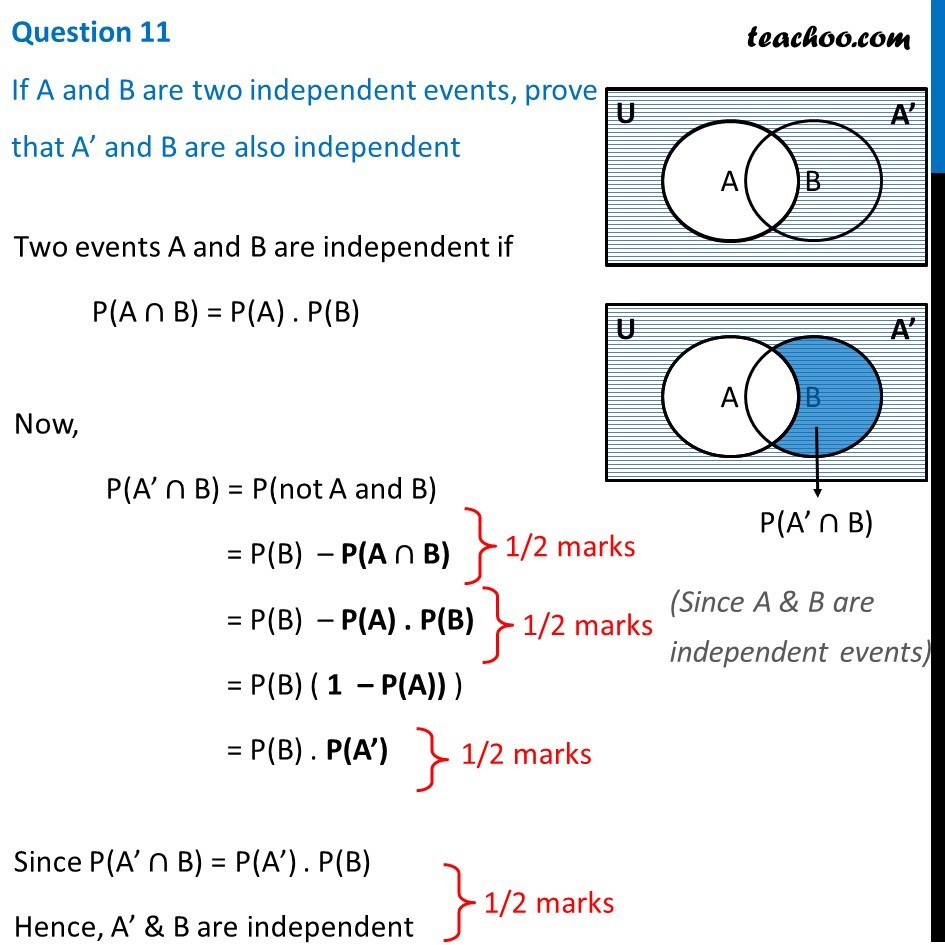
Events A and B are independent if: knowing whether A occured does not change the probability of B. Mathematically, can say in two equivalent ways: P(B|A) = P(B) P(A and B)Two events A and B are said to be independent if the fact that one event has occurred does not affect the probability that the other event will occur. If whether or not one event occurs does affect the probability that the other event will occur, then the two events are said to be dependent.Explanation: Independent Events: Two events A & B are said to be independent if occurrence or non-occurrence of one does not affect the probability of the occurrence or non-occurrence of the other.
Learn more about the topic Are the events A and B independent.
- Events A and B are independent if – UC Berkeley Statistics
- Conditional Probability and Independence – Biostatistics
- [Solved] If A and B are two independent events then – Testbook
- Lesson Explainer: Dependent and Independent Events | Nagwa
- 3.2 Independent and Mutually Exclusive Events – Statistics
- Basic Concepts in Probability – Online Statistics Book
See more: khoaluantotnghiep.net/travel